すなわち、グループ間比較に対する仮説検定でP＜0.05、と「有意差あり」であった場合、グループ間差に対しての95％信頼区間を求めると、0を含みません。一方、仮説検定でP＞0.05、と「有意差なし」であった場合、95％信頼区間は0を含む、すなわち95％信頼区間の下限値はマイナスに、上限値はプラスになるということです。

例えば高血圧を有する60人の患者さんを2グループに分け、1グループで新しい降圧薬Aを、もう一方のグループで従来からの降圧薬Bを投与し、血圧の低下に差があるかどうかを検討したとしましょう。そしてその結果をまとめたのがつぎの表であったとしましょう。

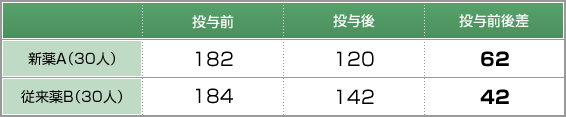
この結果から、収縮期血圧の低下度(投与前後の差)に関して、グループ間に有意差があるかどうかを調べるため、仮説検定をあてはめると、

となりました。このことより、新薬Aは従来薬Bに比べ、有意に大きく血圧を低下させた、と解釈することができます。

つぎにグループ間差の95％信頼区間を計算するとつぎの通りになりました。

となりました。このことより、新薬Aは従来薬Bに比べ、有意に大きく血圧を低下させた、と解釈することができます。

これらのことより、解釈としては…

となります。このように、仮説検定でP＜0.05のときには信頼区間は0を含んでいません。

では他の例として、2種類の新薬AとCの比較をするとつぎのようになったとしましょう。

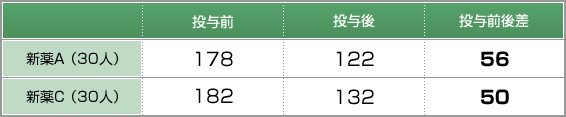
このデータに対して、グループ間に対して仮説検定を当てはめた結果、

となりました。この結果から、新薬AとCとでは、血圧の低下作用に有意差がない、と解釈できます。

つぎに、収縮期血圧の低下度のグループ間差に対する95％信頼区間を求めると

となりました。このことから…

と解釈できます。“-6mmHg大きく低下させる”というのは日本語してわかりにくいので、わかりやすいように書き換えるとつぎのようになります。

すなわち、薬Aが薬Cに比べより大きく血圧を低下させる可能性があると同時に、逆に薬Cが薬Aに比べより大きく血圧を低下させる可能性もあるため、薬Aと薬Cのどちらが血圧をより大きく低下さえるかの判断ができない、ということになります。

この例の場合、仮説検定の結果、有意差なし(P≧0.05)で、95％信頼区間は0を含んでいるので、仮説検定と信頼区間の関係がやはりこの例でも正しくなっています。

さて、この仮説検定と信頼区間の密接な関係から、つぎの重要ポイントを知っておくと便利です。

すなわち、95％信頼区間を求めることによって、グループ間の差がどのくらいあるのか、ということのみならず、グループ間の差は有意かどうかも知ることが可能となります。このことから、信頼区間の情報は、仮説検定から得られる情報に比べてより有用であると言えます。

これまでの医学研究の報告では、P値という仮説検定の結果のみが重要視されて、信頼区間が示されていなかったことが多かったと言えます。しかし、P値の正しい解釈は意外と容易でなく、研究者、読者ともにしばしば誤った解釈をしてしまっているというのも確かです。とくに、有意差さえあれば信頼のできる研究で、一方有意差が出ていない研究は読む必要もない、と考えられる傾向にあります。この有意差が「ある・なし」の判定はあまりに単純な発想で、今のように進化した臨床の現場ではそのような二元論的な情報はあまり役に立たないと考えるべきでしょう。差が「ある・なし」のみではなく、「どれほどの差があるのか？」を示す信頼区間を正確に解釈して、臨床の現場に役立たせるべきでしょう。