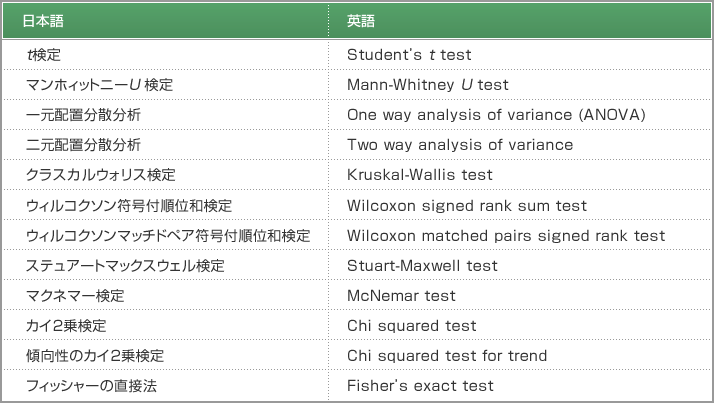
• (浅井 隆、いまさら誰にも聞けない. 医学統計の基礎のキソ1、アトムス出版、2010年から転載)
• 統計を使用する研究者は、どういうデータにはどの統計法を使うかを適切に選択する必要がありますが、これら仮説検定の結果の基本的解釈の仕方はどれも同じです。その理由は簡単で、

だからです。すなわちP値の解釈ができればよいことになります。論文の結果で、P値はつぎのように示されます。

このように結果に書かれたP値の基本的な解釈はむずかしくありません。

• これでP値、すなわち仮説検定結果の解釈は基本的にできたことになります。
• ではここで、P値とか、P=0.07とかP＜0.05とか、これらの数字や記号が何を意味しているかを確かめておきましょう。

となります。すなわち、仮説検定に関するある確率を示したものです。P値の場合、確率は0.05のように小数点で示されています。これはつぎのようにパーセントに変更が可能です。

ここまでは簡単に理解できると思います。ではこれからP値の意味を見ていきましょう。P値は仮説検定の結果を数字で示したものです。ですから、まずは仮説検定が何かを知る必要があります。

• 仮説検定は、グループ間の比較をする場合、例えば「新薬Aは従来薬Bに比べてより大きく心拍数を減少させるはずである」という仮説が得られたデータから支持されるかどうかを統計学的に見るものです。すなわち、「得られたグループ間の差は条件の違い(この場合、新薬Aが投与されたか、それとも従来薬Bが投与されたか)によるのであって、個体差(偶然の差)によるものではない」ことを調べます。
• しかし、統計学的には、条件の違いによるグループ差から個体差を取り除くことは技術的に困難であるため、実際には、

という発想から調べることになります。すなわち…

• という前提に立って調べていきます。このように、「条件差がない」という概念を帰無仮説と呼び、この帰無仮説に基づいてグループ間に本当に差がないかどうかを調べる方法を仮説検定と呼びます。
• そして、P値の解釈は、

• となります(統計学的に正しく解釈すると、P値は「帰無仮説が正しいとした場合で、得られたデータ結果の差が起こりうる確率を示している」となりますが、理解しやすいように解釈を飛躍させてあります)。
• 当然ながら、立てられた仮説は「グループ間の差は、条件の違い(この場合、新薬Aが投与されたか、それとも従来薬Bが投与されたか)による」というものですから、P値、すなわち帰無仮説が正しい確率が低ければ低い方が、仮説が正しい信頼性が高くなります。一般的には、P値が5％未満の場合(すなわちP＜0.05)、仮説が支持されたと解釈します。
• 医学研究では多くの場合、0.05未満で「有意差あり」としています。ただ、時々0.01、場合によっては0.016未満などで「有意差あり」とすることがあります。そのため、有意差のあるなしを0.05未満にしたのか、それとも他の数値未満にしたのかが、研究論文の方法に定義されているはずです。この「有意差あり・なし」の判定に用いた方の数字(0.05や0.01など)を有意水準と呼んでいます。