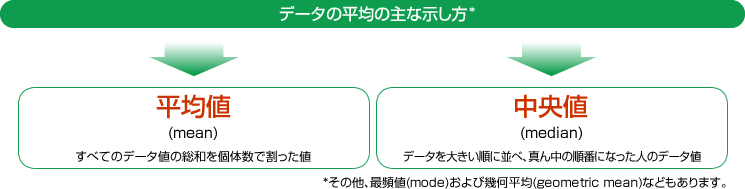
• まずつぎの例を見て下さい。21人からあるデータを収集したところ、結果はつぎの通りになったとしましょう。

このデータから平均値と中央値を求めると…

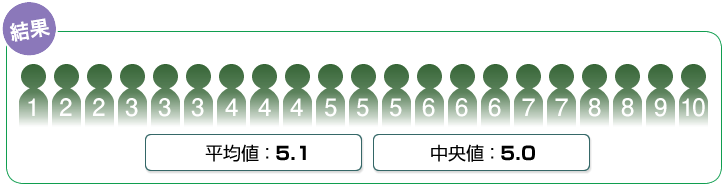
• というように、平均値も中央値もだいたい同じ値になっています。しかし、この例の結果を見ても使い分け方はあまりわかりません。
• ではつぎの例を見てください。21人からのデータ結果はつぎの通りだったとしましょう。

このデータから平均値と中央値を求めると…

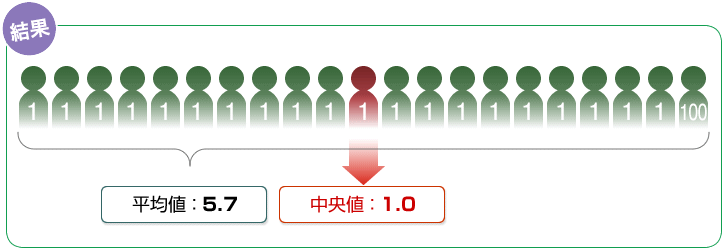
• というように、今度は平均値と中央値がずいぶん違っています。
• これらの2つの例から言えることは、1つ目の例のように、データがまんべんなく広がっているときは、平均値と中央値は同じような値になります。一方、2つ目の例のように、データが偏っていると、平均値と中央値に大きな差が出ることがあります。さて2つ目の例の結果を見て、平均値と中央値のどちらの方が真ん中(すなわち平均的な値)を示しているように見えるでしょうか？　そうですね、この例の場合、平均値よりも中央値の方がデータの平均的な値を示していると思うはずです。
• これらをまとめると、つぎのようになります。

ばらつき、分布

• 「日本の高校生男子の平均身長が170.2cm」のように、平均値が示されていると有用なことはわかりました。しかし、平均的な値だけでは、平均値以上や以下の結果がどうであったかがよくわかりません。例えば、アパレルメーカーが、平均値のみをデータとして学生服ををつくってしまうと、多くの学生が着たときに丈が短過ぎたり長過ぎたりしてしまいます。そのため、データのばらつき、あるいは分布を知りたいはずです。このばらつきを示すにはいくつかの方法があります。範囲、標準偏差、四分位範囲などです。
• 範囲は文字通り、データがどこからどこまで分布しているか、を示すものです。ですからその結果は、最小値と最大値で示されます。例えば、「対象となった高校生男子100人の身長は、最小154cmから最大186cmまでであった」となります。
• しかし、範囲のみでは、最小値から最大値までの範囲でどのような分布の仕方をしているかがよくわかりません。アパレルメーカーがS、M、Lサイズをそれぞれどの割合でつくればよいかを知りたい時には、平均値と範囲のみのデータ結果では満足しないはずです。これを可能にするのが標準偏差と四分位範囲です。
• 標準偏差は得られたデータの分布を示す方法の1つです。この読み取り方を見てみましょう。例えば男子高校生100人の身長を調べた結果、つぎの通りになったとしましょう。

この標準偏差の解釈の仕方はつぎの通りです。

• この計算法を用いれば、平均値と標準偏差のみで、得られたデータのおおよその分布を計算することができます。例えば、男子高校生の身長の平均値(170.6cm)と標準偏差値(5.2cm)から、データがどのように分布しているか計算してみましょう。
• まずは標準偏差値を2倍します。

この値を平均値に足したり、引いたりします。

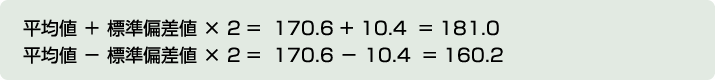
そのため、解釈としては…

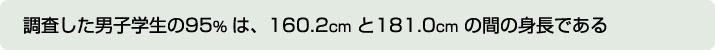
• となります。
• ただし標準偏差に関しては注意点があります。それはつぎの通りです。

データ分布に偏りがある場合には、ばらつきは四分位範囲で示されます。

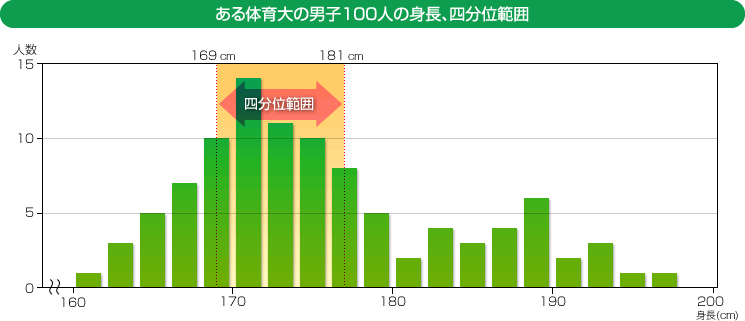
• 四分位範囲はデータに偏りがある場合に、分布を示す方法です。これは、得られたデータの小さい方の25％のデータと、大きい方の25％のデータを捨て、残った中央部50％のデータ範囲を求めたものです。例えば、バスケットボール部で有名な体育大学の学生100人の身長を調査すると、身長の分布は背の高い学生に偏りがあると思われます。そして、その大学生の身長の四分位範囲を統計ソフトで求めると…

• となったとしましょう。この解釈はとしては、身長の高い25％の学生(すなわち背の高い25人)と、身長の低い25％の学生(すなわち背の低い25人)を除いた、中央部50％の学生50人の身長は、169-181cmである、となります。
• データに偏りがある場合、平均値ではなく中央値がより有用なので、平均と分布はつぎのように示されます。

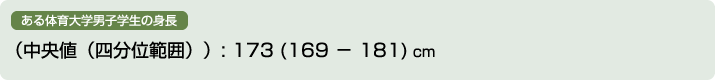
範囲も記載すると…

となります。